Построение графика функции путем сдвига и деформации графика другой функции. Практикум по математическому анализу. Урок 8

Зная график какой-либо функции, можно построить графики многих других более сложных функций чисто геометрическим путем, без составления таблицы числовых значений переменных.
Так, исходя из графика функции $y=f(x)$, можно посредством его сдвига или деформации построить графики для функций вида $y=f(x-a)$, $y=f(x)+b$, $y=Af(x)$, $y=f(kx)$, $y=Af[k(x-a)]+b.$
График функции $y=f(x-a)$ получается из исходного графика путем сдвига его вдоль оси абсцисс на $a$ масштабных единиц этой оси, вправо при $a>0$ и влево при $a<0$ (рис.1). График функции $y=f(x)+b$ получается из исходного графика путем сдвига его вдоль оси ординат на $b$ масштабных единиц этой оси, вверх при $b>0$ и вниз при $b<0$ (рис.1).

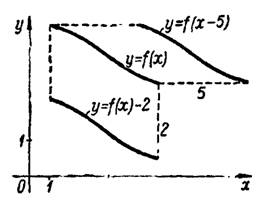
Рис.1

График функции $y=Af(x)$ получается из исходного путем умножения ординат его точек на коэффициент $A$. При этом, если $|A|>1$, то ординаты всех точек исходного графика увеличиваются по абсолютной величине в $|A|$ раз, если $|A|<1$, то они уменьшаются по абсолютной величине в $\displaystyle \frac{1}{|A|}$ раз, если $A<0$, то изменяются еще и их знаки. График функции $y=Af(x)$ при $A<0$ будет симметричен графику функции $y=|A|f(x)$ относительно оси абсцисс (рис.2). График функции $y=f(kx)$ получается из исходного графика путем деления абсцисс его точек на коэффициент $k$. При этом, если $|k|>1$, то абсциссы всех точек исходного графика уменьшаются по абсолютной величине в $|k|$ раз; если $|k|<1$,то они увеличиваются по абсолютной величине в $\displaystyle \frac{1}{|k|}$ раз;

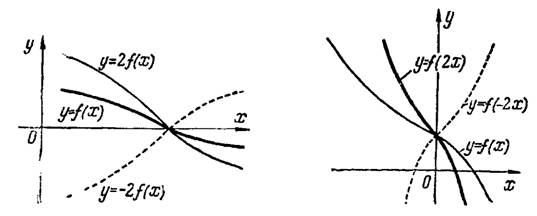
Рис.2                                                                                   Рис.3

если $k<0$, то изменяются еще и их знаки. График функции $y=f(kx)$, при $k<0$, симметричен графику функции$y=f(|k|x)$ относительно оси ординат (рис.3).
Выполняя указанные сдвиги и деформации графика функции $y=f(x)$ в последовательном порядке, одно вслед за другим, можно строить графики и для функций более сложного вида:

$y=Af[k(x-a)]+b.$                                              (1)

Пример 1. Построить по точкам график функции $\displaystyle y=\sqrt{x}$ на отрезке [0; 9] и затем, исходя из этого графика, путем последовательных деформаций его и сдвигов, построить график функции $\displaystyle y=2\sqrt{-3(x+1,5)}-1,2$.
Решение. Составим таблицу соответственных значений переменных $?$ и $y$ для функции $\displaystyle y=\sqrt{x}$ и построим ее график (рис.4).

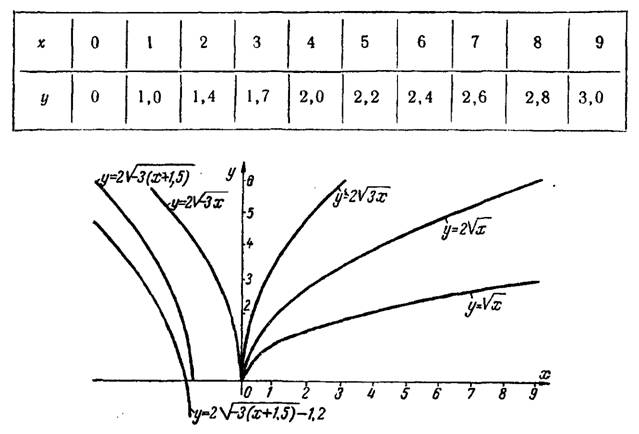
Рис.4

Обозначим функцию $\displaystyle \sqrt{u}$ символом $f(u)$. Тогда данная функция преобразуется к виду

$\displaystyle y=2f[-3(x+1,5)]-1,2.$

Сопоставляя ее с выражением (1), находим следующие значения параметров: $A=2;k=-3;a=-1,5;b=-1,2.$
Далее, согласно общим указаниям, строим искомый график следующим путем:
1) увеличивая в 2 раза ординаты точек графика функции $\displaystyle y=\sqrt{x}$ и сохраняя неизменными их абсциссы, строим график функции $\displaystyle y=2\sqrt{x}$;
2) уменьшая в Зраза абсциссы точек графика функции $\displaystyle y=2\sqrt{x}$ и сохраняя неизменными их ординаты, строим график функции $\displaystyle y=2\sqrt{3x}$;
3) меняя знаки у абсцисс точек графика функции $\displaystyle y=2\sqrt{3x}$ и сохраняя неизменными их ординаты, строим график функции $\displaystyle y=2\sqrt{-3x}$ (графики функций $\displaystyle y=2\sqrt{3x}$ и $\displaystyle y=2\sqrt{-3x}$ симметричны относительно оси ординат);
4) перенося точки графика функции $\displaystyle y=2\sqrt{-3x}$ в направлении оси абсцисс на 1,5 единицы масштаба этой оси влево, строим график функции $\displaystyle y=2\sqrt{-3(x+1,5)}$;
4) перенося точки графика функции $\displaystyle y=2\sqrt{-3(x+1,5)}$ в направлении оси ординат на 1,2 единицы масштаба этой оси вниз, строим искомый график функции у-=2 $\displaystyle y=2\sqrt{-3(x+1,5)}-1,2$.
Пример 2. Исходя из графика функции $\displaystyle y=\sin x$, путем его деформаций и сдвигов построить график функции $\displaystyle y=-3\sin (2x+8).$
Решение. Заменяя в выражении (1) символ произвольной функции $f$ символом тригонометрической функции $sin$, получим

$\displaystyle y=A\sin k(x-a)+b.$                                 (2)

Преобразуем данную функцию:

$\displaystyle y=-3\sin (2x+8)=-3\sin (x+4)$

и, сопоставляя ее с выражением (2), определим следующие значения параметров: $A=-3; k=2; a=-4; b=0.$
Построение искомого графика выполняем, руководствуясь общими указаниями:
1) увеличивая в 3 раза ординаты точек графика функции $\displaystyle y=\sin x$ по абсолютной величине, меняя их знаки и сохраняя неизменными абсциссы, строим график функции $\displaystyle y=-3\sin x$ (рис.5);
2) уменьшая в 2 раза абсциссы точек графика функции $\displaystyle y=-3\sin x$ и сохраняя неизменными их ординаты, строим график функции $\displaystyle y=-3\sin 2x$;

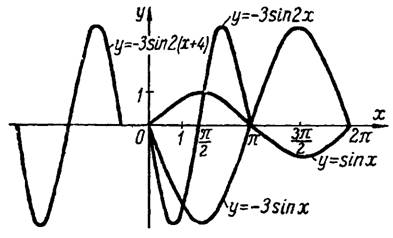
Рис.5

3) перенося точки графика функции $\displaystyle y=-3\sin 2x$ в направлении оси абсцисс на 4 единицы масштаба этой оси влево, строим искомый график функции $\displaystyle y=-3\sin 2(x+4)$.
Пользуясь периодичностью данной функции, полученный график можно продолжить в обе стороны.