Пример 3. Доказать, что:
1)  .
.
2)  .
.
Решение.
1) Составим разность  . При
. При  эта разность является бесконечно малой, как величина, обратная бесконечно большой. А если переменная
эта разность является бесконечно малой, как величина, обратная бесконечно большой. А если переменная  отличается от постоянной
отличается от постоянной  на величину бесконечно малую, то постоянная является пределом переменной. Следовательно,
на величину бесконечно малую, то постоянная является пределом переменной. Следовательно,  .
.
2) Положим  и составим разность:
и составим разность: ![\displaystyle (2x+1)-7=[2(3+\alpha)+1]-7=2\alpha](https://math-helper.net/wp-content/plugins/latex/cache/tex_f9ad53fab3e26f45e01eb9fe9962c1e4.gif) . При
. При  переменная
переменная  и разность между функцией
и разность между функцией  и числом 7, т. е.
и числом 7, т. е.  , будет бесконечно малой. Из этого следует, что
, будет бесконечно малой. Из этого следует, что  .
.
Пример 4. Найти пределы функции  :
:
1) при  ;
;
2) при  .
.
Пояснить решение таблицами.
Решение. 1) Если  будет стремиться к 2 слева, оставаясь меньше 2, то
будет стремиться к 2 слева, оставаясь меньше 2, то  будет положительная бесконечно малая, a
будет положительная бесконечно малая, a  будет положительная бесконечно большая, т. е. если
будет положительная бесконечно большая, т. е. если  , то
, то  , а
, а  , или
, или  .
.
Указанное поведение переменных  и
и  поясняется следующей таблицей:
поясняется следующей таблицей:
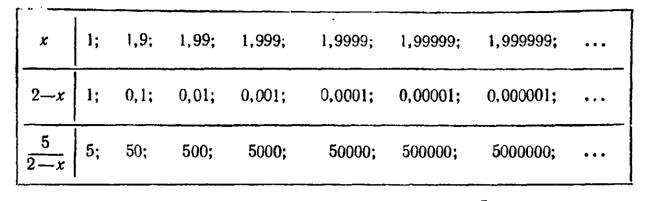
2) Если  , то
, то  , a
, a  или
или  .
.
Таблица соответствующих значений переменных  и
и  наглядно показывает их поведение:
наглядно показывает их поведение:

График функции  изображен на рис. 1.
изображен на рис. 1.
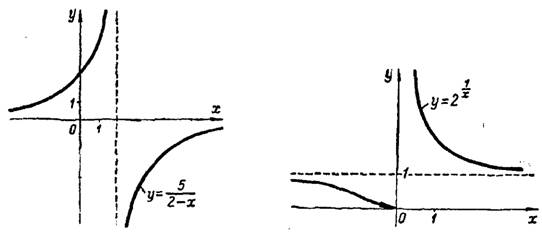
Рис.1 Рис.2
Пример 5. Найти пределы функции  при
при  , стремящемся к нулю: 1) слева, 2) справа и 3) произвольным способом.
, стремящемся к нулю: 1) слева, 2) справа и 3) произвольным способом.
Решение. 1) Если переменная  будет стремиться к нулю слева, оставаясь отрицательной, т. е. если
будет стремиться к нулю слева, оставаясь отрицательной, т. е. если  будет отрицательной бесконечно малой, то
будет отрицательной бесконечно малой, то  будет отрицательной бесконечно большой и
будет отрицательной бесконечно большой и  , что следует из решения задачи 2 (урок 10).
, что следует из решения задачи 2 (урок 10).
2) Если  , то
, то  и
и  .
.
3) Если  будет стремиться к нулю произвольным способом, не оставаясь с одной стороны от него (например, как
будет стремиться к нулю произвольным способом, не оставаясь с одной стороны от него (например, как  в задаче 1(урок 10) ), то
в задаче 1(урок 10) ), то  будет стремиться к бесконечности, принимая значения разных знаков. Вследствие этого при
будет стремиться к бесконечности, принимая значения разных знаков. Вследствие этого при  функция
функция  не имеет предела, не будучи при этом и бесконечно большой величиной
не имеет предела, не будучи при этом и бесконечно большой величиной  не существует.
не существует.
График функции  показан на рис. 2.
показан на рис. 2.
Пример 6. Найти пределы функции  : 1) при
: 1) при  ; 2) при
; 2) при  и 3) при
и 3) при  .
.
Решение.
1) Если  , то
, то  , a
, a  , т. е.
, т. е.  .
.
2) Если  , то
, то  , a
, a  , т. е.
, т. е.  .
.
3) Если  , то
, то  , a
, a  не стремится ни к какому значению, т. е.
не стремится ни к какому значению, т. е.  не существует,
не существует,
График этой функции показан на рис. 3.
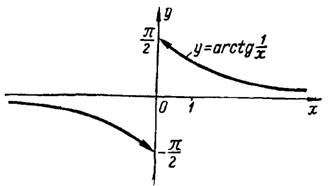
Рис. 3







