Применение определенного интеграла в физике. Практикум по математическому анализу. Урок 89

Пример 1. Определить давление воды на вертикальный прямоугольный шлюз с основанием 18 м и высотой 6 м.
Решение. Величина $p$ давления жидкости на горизонтальную площадку зависит от глубины ее погружения $x$, т. е. от расстояния площадки до поверхности жидкости: $\rho =\delta ax$; $\delta$ — удельный вес жидкости, $a$ — площадь площадки.

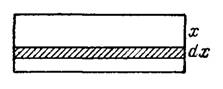
Рис. 1

Руководствуясь общей схемой (II) применения определенного интеграла к вычислению величин, разделим шлюз на глубине $x$ горизонтальной прямой (рис. 1). Тогда давление воды на верхнюю часть шлюза будет некоторой функцией $p(x)$. Найдем дифференциал $dp$ этой функции, т. е. приближенную величину (главную часть) ее приращения $\Delta p$ при изменении глубины $x$ на малую величину $dx$.
Допустим, ввиду малости $dx$, что все точки заштрихованной полоски находятся на глубине $x$, т. е. что она расположена на глубине $x$ в горизонтальной плоскости. Тогда приближенная величина давления воды на эту полоску будет равна весу столба воды, имеющего основанием эту полоску, и высотой — глубину $x$:
$\Delta p\approx dp=18\delta x\, dx=18x\, dx.$ (Удельный вес воды $\delta =1$.)
Согласно условию задачи глубина $x$ изменяется на отрезке $0\leq x\leq 6$. Поэтому искомое давление $P$ на весь шлюз найдем, интегрируя $dp$ в пределах от 0 до 6:

$$\displaystyle P=18\int_{0}^{6}xdx=9x^{2} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{6}=324T\approx 324000\cdot 9,81H\approx 3178440H\approx 3,18MH.$$

Пример 2. При условиях предыдущей задачи найти, на какой глубине $x=c$ надо разделить шлюз горизонтальной прямой, чтобы давление воды на верхнюю и нижнюю части шлюза было одинаково.
Решение. Определим давление воды на каждую часть шлюза, интегрируя $dp$ в пределах от 0 до $c$ и в пределах от $c$ до 6, затем приравниваем интегралы друг другу:

$$\displaystyle 18\int_{0}^{c}xdx=18\int_{c}^{6}xdx;\; x^{2} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{c}=x^{2} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{c}^{6};\; c^{2}=36-c^{2}.$$

Решая полученное уравнение, найдем $c=3\sqrt{2}\approx 4,23$ м.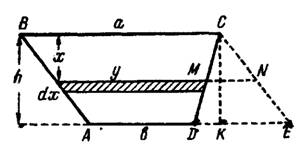

Рис. 2

Пример 3. Определить давление воды на вертикальную плотину, имеющую форму трапеции, размеры которой указаны на рис. 2.
Решение. Допуская, что заштрихованная полоска расположена на глубине $x$ в горизонтальной плоскости и что она является прямоугольником со сторонами $y$ и $dx$, найдем приближенную величину давления воды на эту полоску $\Delta p\approx xy\, dx=dp$ и затем давление воды на всю плотину: $\displaystyle P=\int_{0}^{h}xy\, dx.$
Для вычисления интеграла выразим переменную $y$ через переменную $x$. Проведя вспомогательную прямую $CE$ параллельно $BA$ из подобия треугольников $DCE$ и $MCN$ имеем пропорцию

$$(a-b):(a-y)=h:x,$$

из которой находим $\displaystyle y=a-\frac{x}{h}(a-b).$
Подставляя в подынтегральное выражение и интегрируя, получим

$$\displaystyle P=\int_{0}^{h}x\left ( a-\frac{x}{h}(a-b) \right )dx=a\int xdx-\frac{a-b}{h}\int x^{2}dx \left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{h}=\frac{h^{2}(a+2b)}{6}.$$

Пример 4. Найти давление воды на поверхность шара диаметром 4 м, если его центр находится на глубине 3 м от поверхности воды.
Решение. Проведем через центр шара вертикальную плоскость и выберем на ней прямоугольную систему координат $xOy$, как показано на рис. 3.

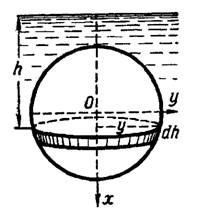
Рис. 3

Рассечем шар на глубине $h$ горизонтальной плоскостью. Тогда давление воды на отсеченную часть поверхности шара будет некоторой функцией $p(h)$.
При изменении $h$ на величину $dh$ площадь $S$ отсеченной части поверхности шара, как площадь поверхности вращения вокруг оси $Ox$, изменится на величину $\Delta s\approx 2\pi y\, dl=ds$, где $dl$ — дифференциал дуги окружности, а давление $p(h)$ изменится на величину $\Delta p\approx 2\pi hy\, dl=dp.$

Выразив $dp$ через одну переменную $x$ и интегрируя в пределах от $x=-2$ до $x=2$, найдем давление воды на всю поверхность шара. Из уравнения окружности $x^{2}+y^{2}=4$ найдем $\displaystyle y'=-\frac{x}{y}$ и затем $\displaystyle dl=\sqrt{1+(y')^{2}}dx=\sqrt{1+\frac{x^{2}}{y^{2}}}dx=\frac{2}{y}dx;$ из чертежа находим $h=3+x.$ Следовательно,

$$\displaystyle P=2\pi \int_{-2}^{2}(3+x)y\frac{2}{y}dx=4\pi \int_{-2}^{2}(3+x)dx=2\pi (3+x)^{2} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{-2}^{2}=48\pi T\approx 470880\pi H\approx 0,471\pi MH.$$

Давление на верхнюю половину поверхности шара получим, интегрируя $dp$ в пределах от —2 до 0:

$$\displaystyle P_{1}=2\pi (3+x)^{2} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{-2}^{0}=16\pi (T)\approx 156960\pi (H)\approx 0,157\pi MH.$$

Давление на нижнюю половину поверхности шара будет

$$\displaystyle P_{2}=2\pi (3+x)^{2} \left.\begin{matrix} \\ \\ \end{matrix}\right| _{0}^{2}=32\pi (T)\approx 313920\pi (H)\approx 0,314\pi MH.$$