Прямая линия в пространстве. Основные формулы

1. Общие уравнения прямой.
Прямая линия в пространстве определяется как линия пересе­чения двух плоскостей. В этом случае она определяется системой двух уравнений первой степени:

$$\left\{\begin{matrix} A_{1}x+B_{1}y+C_{1}z+D_{1}=0,\\ A_{2}x+B_{2}y+C_{2}z+D_{2}=0. \end{matrix}\right.\; \; \; (1)$$

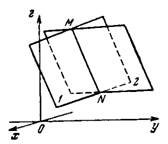
Уравнения (1), рассматриваемые совместно, называются общими уравнениями прямой (рис.1).

2. Уравнения прямой в двух проектирующих плоскостях.
Уравнения прямой в проекциях на координатные плоскости, например, на плоскости хОz и yOz имеют вид:

$$\left\{\begin{matrix} x=Mz+a,\\ y=Nz+b. \end{matrix}\right.\; \; \; \; (2)$$

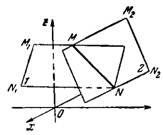
Уравнения (2) можно также назвать уравнениями прямой в двух проектирующих плоскостях, первая из которых перпендикуляр­на плоскости xOz, вторая перпендикулярна плоскости yOz (рис.2).

3. Канонические уравнения прямой линии

$$\frac{x-a}{m}=\frac{y-b}{n}=\frac{z-c}{p}\; \; \; (3)$$

где а; Ь; с — координаты точки $M_{0}$, лежащей на прямой линии;
х; у; z — текущие координаты точек прямой;
m; n; p — направляющие коэффициенты, пропорциональные на­правляющим косинусам прямой:

$$m:n:p=\cos \alpha :\cos \beta :\cos \gamma .$$

Направляющие косинусы определяются по формулам:

$$\cos \alpha =\pm \frac{m}{\sqrt{m^{2}+n^{2}+p^{2}}},\; \cos \beta =\pm \frac{n}{\sqrt{m^{2}+n^{2}+p^{2}}},\; (4)$$

$$\cos \gamma =\pm \frac{p}{\sqrt{m^{2}+n^{2}+p^{2}}}.\; \;$$

В формулах (4) можно брать знак плюс или минус соответствен­но двум противоположным направлениям прямой.
4. Параметрические уравнения прямой линии.

$$\left\{\begin{matrix} x=mt+a,\\ y=nt+b,\\ z=pt+c, \end{matrix}\right.\; \; \; (5)$$

где а; Ь; с — координаты точки $M_{0}$, лежащей на прямой;
х; у; z — текущие координаты точек прямой;
m; n; p — направляющие коэффициенты; t — переменный параметр.
5. Уравнения прямой, проходящей через две данные точки $M_{1}(x_{1};y_{1};z_{1})$ и $M_{2}(x_{2};y_{2};z_{2})$:

$$\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}.\; \; \; (6)$$

6. Векторное уравнение прямой линии

$$\vec{r}=\vec{r_{0}}+\vec{S}t,\; \; \; (7)$$

$\vec{r}\left\{x,y,z \right\},\; \vec{r_{0}}\left\{a;b;c \right\}$ — радиусы-векторы точек $M(x;y;z)$ и
$M_{0}(a;b;c)$ на прямой;
$\vec{S}\left\{m;n;p \right\}$ — направляющий вектор, параллельный данной прямой;
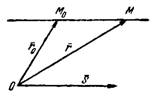
t — переменный параметр (рис.3).

Пусть прямая задана общими уравнениями

$$\left\{\begin{matrix} A_{1}x+B_{1}y+C_{1}z+D_{1}=0,\\ A_{2}x+B_{2}y+C_{2}z+D_{2}=0. \end{matrix}\right.\; \; \; (1)$$

тогда за ее направляющий вектор $\vec{S}$ можно принять векторное про­изведение $\vec{n_{1}}\times \vec{n_{2}}$ векторов $\vec{n_{1}}(A_{1},B_{1},C_{1})$ и $\vec{n_{2}}(A_{2},B_{2},C_{2})$, так как каждый из них перпендикулярен этой прямой и, следовательно, век­тор $\vec{n_{1}}\times \vec{n_{2}}$ параллелен ей.
Таким образом, направляющий вектор прямой (1) определяется:

$$\vec{S}=\left[\vec{n_{1}} \vec{n_{2}}\right]=\begin{vmatrix} \vec{i} & \vec{j} & \vec{k}\\ A_{1} & B_{1} & C_{1}\\ A_{2} & B_{2} & C_{2} \end{vmatrix}.\; \; \; (8)$$

7. Угол между двумя прямыми
$\frac{x-a_{1}}{m_{1}}=\frac{y-b_{1}}{n_{1}}=\frac{z-c_{1}}{p_{1}}$ и $\frac{x-a_{2}}{m_{2}}=\frac{y-b_{2}}{n_{2}}=\frac{z-c_{2}}{p_{2}}$
определяется по формуле

$$\cos \phi =\pm \frac{m_{1}m_{2}+n_{1}n_{2}+p_{1}p_{2}}{\sqrt{m^{2}_{1}+n^{2}_{1}+p^{2}_{1}}\cdot \sqrt{m^{2}_{2}+n^{2}_{2}+p^{2}_{2}}}.\; \; (9)$$

В формуле (9) можно взять любой знак, что соответствует выбору одного из двух смежных углов между данными прямыми.
8. Условие параллельности двух прямых имеет вид:

$$\frac{m_{1}}{m_{2}}=\frac{n_{1}}{n_{2}}=\frac{p_{1}}{p_{2}}.\; \; (10)$$

9. Условие перпендикулярности двух прямых имеет вид:

$$m_{1}m_{2}+n_{1}n_{2}+p_{1}p_{2}=0.\; \; \; (11)$$