Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (рис. 1) по формуле

где
 и
и  — угловые коэффициенты касательных к кривым в точке их пересечения
— угловые коэффициенты касательных к кривым в точке их пересечения  ,
,т. е. частные значения в точке
 производных от
производных от  по
по  из уравнений этих кривых:
из уравнений этих кривых:
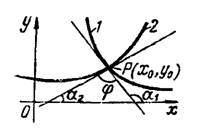
Рис.1
Пример 1. Найти углы, под которыми пересекаются следующие линии:
1) прямая  и парабола
и парабола  ;
;
2) эллипс  и парабола
и парабола  ;
;
3) синусоида  и косинусоида
и косинусоида  .
.
Решение.
1) Совместно решая уравнения параболы и прямой, находим, что они пересекаются в двух точках:  и
и  , рис.2.
, рис.2.
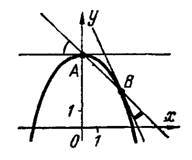
Рис.2
Далее находим производную от  по
по  из уравнения параболы:
из уравнения параболы:  и определяем угловые коэффициенты касательных к параболе в точках
и определяем угловые коэффициенты касательных к параболе в точках  и
и  , как частные значения этой производной:
, как частные значения этой производной:

Угловой коэффициент прямой один и тот же во всех ее точках; у данной прямой он равен — 1.
Согласно формуле (2) получим

2) Решая совместно уравнения кривых, находим их общие точки:
 и
и  рис.3. Затем определяем угловые коэффициенты
рис.3. Затем определяем угловые коэффициенты  и
и  касательных в любой точке эллипса и параболы как производные от
касательных в любой точке эллипса и параболы как производные от  по
по  из их уравнений
из их уравнений
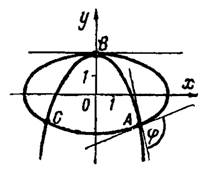
Рис.3
Подставляя координаты точки  , получим
, получим  и
и  . Следовательно, в точке
. Следовательно, в точке  :
:

Под таким же углом кривые пересекаются и в точке
 вследствие их симметричности относительно оси
вследствие их симметричности относительно оси  .
.В точке
 имеем:
имеем:  , следовательно, в точке
, следовательно, в точке  кривые имеют общую касательную, т. е. касаются друг друга. В этой точке угол между кривыми равен нулю.
кривые имеют общую касательную, т. е. касаются друг друга. В этой точке угол между кривыми равен нулю.3) Абсциссы точек пересечения кривых (рис.4) определяются уравнением
 , решая которое, получим
, решая которое, получим
Дифференцированием находим угловые коэффициенты касательных к синусоиде и косинусоиде:

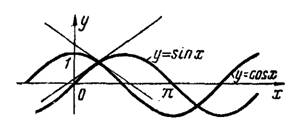
Рис.4
Искомый угол между кривыми определяем по общей формуле (2)

Положительному знаку соответствует острый угол  , отрицательному — тупой, смежный с ним угол
, отрицательному — тупой, смежный с ним угол  .
.







