Касательная и нормаль к плоской кривой. Практикум по математическому анализу. Урок 35

Если плоская кривая отнесена к прямоугольной системе координат (рис. 1), то уравнения касательной и нормали к ней в точке $\displaystyle M(x_{0},y_{0})$ имеют вид:

$$\displaystyle y-y_{0}=y_{0}(x-x_{0});\; y-y_{0}=-\frac{1}{y'_{0}}(x-x_{0}),\; \; (1)$$

где $\displaystyle y'_{0}$ — значение в точке $\displaystyle x_{0}$ производной $\displaystyle \frac{dy}{dx}$ из уравнения кривой.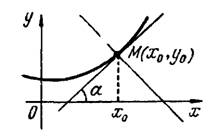

Рис.1

Направление кривой в каждой ее точке определяется направлением касательной к ней в этой точке. Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (рис. 2) по формуле

$$\displaystyle tg\: \varphi =\frac{k_{1}-k_{2}}{1+k_{1}k_{2}},\; \; (2)$$

где $\displaystyle k_{1}$ и $\displaystyle k_{2}$ — угловые коэффициенты касательных к кривым в точке их пересечения $\displaystyle P(x_{0},y_{0})$,

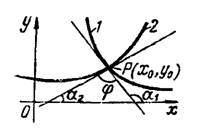
Рис.2

т. е. частные значения в точке $\displaystyle x_{0}$ производных от $y$ по $x$ из уравнений этих кривых:

$$\displaystyle k_{1}=tg\: \alpha _{1}=\left ( \frac{dy_{1}}{dx} \right )_{x=x_{0}};\; k_{2}=tg\: \alpha _{2}=\left ( \frac{dy_{2}}{dx} \right )_{x=x_{0}}.$$

Пример 1. Составить уравнения касательной и нормали:
1) к параболе $\displaystyle y=x^{2}-4x$ в точке, где $x=1$;
2) к окружности $\displaystyle x^{2}+y^{2}-2x+4y-3=0$ в точках пересечения ее с осью $Ox$;
3) к циклоиде $\displaystyle x=t-\sin t,\: y=1-\cos t$ в точке, где $\displaystyle t=\frac{\pi }{2}$.
4) к кривой $\displaystyle y=\left | x^{3}-1 \right |$ в ее угловой точке.
Решение. 1) Подставляя в уравнение параболы заданную абсциссу точки касания $x=1$, найдем ее ординату $y=-3$.
Для определения углового коэффициента касательной $\displaystyle y'_{0}$ находим производную от $y$ по $x$ из уравнения параболы и вычисляем ее частное значение в точке $x=1$:

$$\displaystyle y'=2x-4;\; y'_{0}=y'(1)=-2.$$

Подставляя значения $\displaystyle x_{0},y_{0}$ и $\displaystyle y'_{0}$ в общие уравнения (1), получим уравнение касательной
$\displaystyle y+3=-2(x-1)$ или $\displaystyle 2x+y+1=0$
и уравнение нормали
$\displaystyle y+3=\frac{1}{2}(x-1)$ или $\displaystyle x-2y-7=0$.
Парабола, касательная и нормаль построены на рис.3.

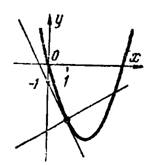
Рис.3

2) Решая совместно заданное уравнение окружности и уравнение оси $Ox,$ $y=0$, находим точки их пересечения: $\displaystyle A(-1;0),B(3;0)$ рис.4.

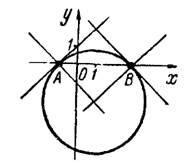
Рис.4

Дифференцируя по $x$ уравнение окружности

$$\displaystyle 2x+2yy'-2+4y'=0$$

,
находим производную $\displaystyle y'=\frac{1-x}{2+y}$ и вычисляем ее значения для точек $A$ и $B$: $\displaystyle y'_{A}=1,\: y'_{B}=-1.$
Подставляя в общие уравнения (1), получим искомые уравнения касательной и нормали:
для точки $A$ соответственно $\displaystyle x-y+1=0$ и $\displaystyle x+y+1=0$;
для точки $B$ $\displaystyle x+y-3=0$ и $\displaystyle x-y-3=0$.
3) Подставляя в уравнения циклоиды $\displaystyle t=\frac{\pi }{2}$ находим координаты точки касания: $\displaystyle x=\frac{\pi }{2}-1;\: y=1.$
Затем определяем производную от $y$ по $x$ из уравнений циклоиды, как от функции, заданной параметрически

$$\displaystyle y'=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{\sin t}{1-\cos t}=\frac{2\sin \frac{t}{2}\cos \frac{t}{2}}{2\sin ^{2}\frac{t}{2}}=\textrm{ctg}\: \frac{t}{2},$$

и вычисляем ее значение для точки касания $\displaystyle y'_{0}=y'\left ( \frac{\pi }{2} \right )=1.$
Подставляя значения $\displaystyle x_{0},y_{0}$ и $\displaystyle y'_{0}$ в уравнения (1), получим уравнение касательной $\displaystyle 2x-2y-\pi +4=0$ и уравнение нормали $\displaystyle 2x+2y-\pi =0$.
4) Найдем производную $y'$ и затем угловую точку данной кривой из условия, что для этой точки производная $y'$ не существует, но существуют различные односторонние производные:

$$\displaystyle y'=\left | x^{3}-1 \right |'=\pm 3x^{2},$$

где плюс соответствует интервалу $\displaystyle x>1$, в котором $\displaystyle x^{3}-1>0$, а минус — интервалу $\displaystyle x<1$, где $\displaystyle x^{3}-1<0$. Отсюда заключаем, что точка, где $x=1$ является угловой; в этой точке кривая имеет две односторонние касательные с угловыми коэффициентами $\displaystyle k_{1}=\underset{\Delta x \to -0}{lim}\frac{\Delta y}{\Delta x}=y'_{(-)}(1)=-3$ и $\displaystyle k_{2}=\underset{\Delta x \to +0}{lim}\frac{\Delta y}{\Delta x}=y'_{(+)}(1)=3$. Пользуясь общими уравнениями (1), получим уравнения касательных $\displaystyle 3x-y-3=0$ и $\displaystyle 3x+y-3=0$ и уравнения нормалей $\displaystyle x+3y-1=0$ и $\displaystyle x-3y-1=0$ (рис.5).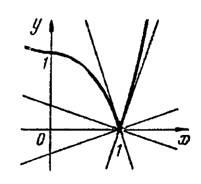

Рис.5