Исследовать функцию и построить график (решение примера). Практикум по математическому анализу. Урок 62

Пример 6. Исследовать функцию $\displaystyle y=x+2\textrm{arcctg}\, x$ и построить ее график.
Решение. I, II. Функция $\displaystyle y=x+2\textrm{arcctg}\, x$ определена и непрерывна на всей числовой оси.
III. Функция не является ни четной, ни нечетной, ни периодической.
V.а) Вертикальных асимптот нет;
б) $\displaystyle k=\underset{x \to \pm \infty}{\lim }\frac{y}{x}=\underset{x \to \pm \infty}{\lim }\left ( 1+\frac{2 \textrm{arcctg}\, x}{x} \right )=1;$
$\displaystyle b_{1}=\underset{x \to +\infty}{\lim }(y-kx)=\underset{x \to +\infty}{\lim }2\textrm{arcctg}x=2\textrm{arcctg}(+\infty)=0;$
$\displaystyle b_{2}=\underset{x \to -\infty}{\lim }(y-kx)=\underset{x \to -\infty}{\lim }2\textrm{arcctg}x=2\textrm{arcctg}(-\infty)=2\pi.$
Следовательно, график функции имеет две невертикальные асимптоты: $y=x$ и $y=x+2\pi$.
VI. $\displaystyle y'=1-\frac{2}{1+x^{2}}=\frac{x^{2}-1}{x^{2}+1}$ существует всюду и обращается в нуль в точках $x=\pm 1$, которые являются критическими. Исследуем эти точки по знаку второй производной:

$$\displaystyle y''=\frac{4x}{(1+x^{2})^{2}};\: y''(-1)<0;\: y''(1)>0.$$

Следовательно, $x=-1$ есть точка максимума, а $x=1$ есть точка минимума: $\displaystyle y_{max}=y(-1)=\frac{3\pi }{2}-1;\: y_{min}=y(1)=\frac{\pi }{2}+1.$
В интервалах $(-\infty ;-1)$ и $(1;+\infty)$, где $y'>0$, функция возрастает, а в интервале $(-1;1)$, где $y'<0$, функция убывает.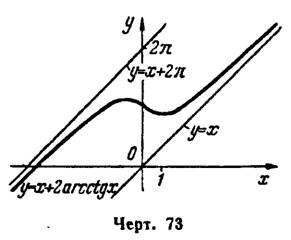
VII. $\displaystyle y''=\frac{4x}{(1+x^{2})^{2}}$ всюду существует и обращается в нуль в точке $x=0$. Определяя знак $y''$ слева и справа от этой точки: $y''(-1)<0$ и $y''(1)>0$, заключаем, что при $x=0$ график функции имеет точку перегиба. Слева от нее, в интервале $(-\infty;0)$, где $y''<0$, график функции обращен выпуклостью вверх, а справа, в интервале $(0;+\infty)$, где $y''>0$, он обращен выпуклостью вниз; $\displaystyle y(0)=\frac{\pi }{2}$.
VIII. Согласно результатам исследования строим график функции (рис. 73).
Пример 7. Исследовать функцию $\displaystyle y=\left | e^{x}-1 \right |$ и построить ее график.
Решение. I, II. Функция $\displaystyle y=\left | e^{x}-1 \right |$ определена и непрерывна на всей числовой оси.
III. Функция не является ни четной, ни нечетной, ни периодической.
IV. Функция всюду неотрицательна; ее график проходит через начало координат.
V. а) Вертикальных асимптот график функции не имеет.
б) При $x\geq 0,\: y=e^{x}-1$, при $x<0,\: y=1-e^{x}$,

$$\displaystyle k=\underset{x \to +\infty }{\lim }\frac{y}{x}=\underset{x \to +\infty }{\lim }\frac{e^{x}-1}{x}=\underset{x \to +\infty }{\lim }\frac{e^{x}}{1}=+\infty,$$

т. е. при $x \to +\infty$ асимптоты нет;

$$\displaystyle k=\underset{x \to -\infty }{\lim }\frac{y}{x}=\underset{x \to -\infty }{\lim }\frac{1-e^{x}}{x}=0,$$

$$\displaystyle b=\underset{x \to -\infty }{\lim }(y-kx)=\underset{x \to -\infty }{\lim }(1-e^{x})=1,$$

т. е. при $x \to -\infty$ график функции имеет невертикальную асимптоту $y=1$. VI. $y'=\pm e^{x}$, где знак плюс соответствует значениям $x$ из интервала $(0;+\infty )$, где $e^{x}-1>0$, а знак минус соответствует значениям $x$ из интервала $(-\infty;0)$, где $e^{x}-1<0$; $y'$ нигде не обращается в нуль и существует всюду, кроме точки $x=0$, которая является критической. Слева от этой точки, где $y'=-e^{x}<0$, функция убывает, а справа от нее, где $y'=e^{x}>0$, функция возрастает. Это значит, что $x=0$ есть точка минимума: $y_{min}=y(0)=0$.
VII. $y''=\pm e^{x}$, где как и у $y'$ знак плюс соответствует значениям $x>0$, а знак минус соответствует значениям $x<0$; $y''$ нигде не обращается в нуль и существует всюду, кроме точки $x=0$. Слева от этой точки, где $y''=-e^{x}<0$, график функции обращен выпуклостью вверх, а справа от нее, где $y''=e^{x}>0$, график функции обращен выпуклостью вниз. Следовательно, $x=0$ есть абсцисса точки перегиба; $y(0)=0$.
Здесь точка перегиба совпала с угловой точкой, в которой график функции имеет две различные односторонние касательные: $y=-x\: y=x$ и минимальное значение ординаты.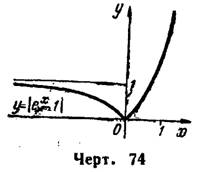

VIII. Для построения графика функ ции дополнительно найдем несколько его точек, например $(1;e-1),\: (-1;1-e^{-1}),\: (-2;1-e^{-2})$ и определим угловые коэффициенты касательных (левую и правую производные) в угловой точке $(0;0)$:

$$k_{1}=y'_{(-)}(0)=-1,\: k_{2}=y'_{(+)}(0)=1.$$

Согласно полученным данным график функции изображен на рис. 74.