1) Графический метод. Отделение корней. Действительные корни уравнения  являются абсциссами точек пересечения кривой
являются абсциссами точек пересечения кривой  с осью
с осью  , а если это уравнение преобразуется к виду
, а если это уравнение преобразуется к виду  , то его действительные корни будут абсциссами точек пересечения кривых
, то его действительные корни будут абсциссами точек пересечения кривых  и
и  .
.
Пользуясь этим, как было показано в решении задачи 2 (урок 7), можно находить приближенные значения действительных корней алгебраических и трансцендентных уравнений путем построения соответствующих кривых.
Однако этим графическим методом можно получить лишь грубо приближенные значения корней уравнения, но нельзя их вычислить с наперед заданной большой точностью.
Поэтому графический метод обычно применяется лишь как вспомогательное средство для определения числа действительных корней уравнения и для их отделения, т. е. для нахождения таких отрезков оси  , внутри которых содержится только по одному корню. Затем, после такого отделения корней, каждый из них может быть вычислен с любой желаемой точностью посредством аналитических методов.
, внутри которых содержится только по одному корню. Затем, после такого отделения корней, каждый из них может быть вычислен с любой желаемой точностью посредством аналитических методов.
2) Уточнение корней уравнения методом хорд и касательных. Если на отрезке ![\left [ a;b \right ]](https://math-helper.net/wp-content/plugins/latex/cache/tex_2e0da052dbfd0bc7073a96b4679e8a6c.gif) функция
функция  непрерывна, а ее производная
непрерывна, а ее производная  сохраняет знак и если
сохраняет знак и если  , то внутри этого отрезка содержится только один действительный корень функции
, то внутри этого отрезка содержится только один действительный корень функции  или уравнения
или уравнения  .
Если, кроме того, на этом отрезке
.
Если, кроме того, на этом отрезке  также сохраняет знак, то можно найти границы
также сохраняет знак, то можно найти границы  и
и  более узкого отрезка, содержащего тот же корень, по формулам
более узкого отрезка, содержащего тот же корень, по формулам

 - тот конец отрезка
- тот конец отрезка ![\left [ a;b \right ]](https://math-helper.net/wp-content/plugins/latex/cache/tex_2e0da052dbfd0bc7073a96b4679e8a6c.gif) , в котором
, в котором  имеет тот же знак, что и
имеет тот же знак, что и  .
. 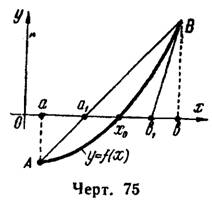
Геометрически (рис. 75) границы нового отрезка
 и
и  представляют абсциссы точек пересечения с осью
представляют абсциссы точек пересечения с осью  хорды
хорды  и касательной
и касательной  , которые будут ближе к искомому корню
, которые будут ближе к искомому корню  , чем границы исходного отрезка
, чем границы исходного отрезка ![\left [ a;b \right ]](https://math-helper.net/wp-content/plugins/latex/cache/tex_2e0da052dbfd0bc7073a96b4679e8a6c.gif) .
.Далее, исходя из полученного суженного отрезка, по тем же формулам (*) можно найти границы
 и
и  еще более узкого отрезка, содержащего в себе корень
еще более узкого отрезка, содержащего в себе корень  .
.Повторяя этот процесс последовательного сужения отрезка, содержащего корень т. е. повторяя применение формул (*), можно найти приближенное значение корня
 с любой заданной точностью.
с любой заданной точностью.Чтобы найти
 с точностью до
с точностью до  , следует вести вычисление
, следует вести вычисление  и
и  до тех пор, когда впервые окажется
до тех пор, когда впервые окажется  или
или 
Тогда, с точностью до  , в первом случае
, в первом случае  (или
(или  ), а во втором случае
), а во втором случае  .
.
Пример 1. Отделить действительные корни следующих уравнений:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Решение. Чтобы отделить действительные корни данного уравнения, т. е. чтобы каждый из них заключить внутри особого небольшого отрезка, воспользуемся графическим методом.
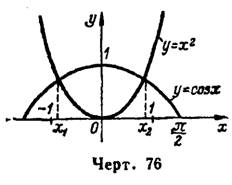
1) Преобразуем данное уравнение к виду  и построим кривые
и построим кривые  и
и  , в одних и тех же координатных осях и при одной и той же единице масштаба (рис. 76).
, в одних и тех же координатных осях и при одной и той же единице масштаба (рис. 76).
Число точек пересечения этих кривых равно числу действительных корней данного уравнения, а их абсциссы являются этими корнями.
Согласно этому положению из чертежа находим: данное трансцендентное уравнение  имеет два действительных корня, один из которых
имеет два действительных корня, один из которых  содержится на отрезке [- 1;- 0,8], а другой
содержится на отрезке [- 1;- 0,8], а другой  на отрезке [0,8; 1].
на отрезке [0,8; 1].
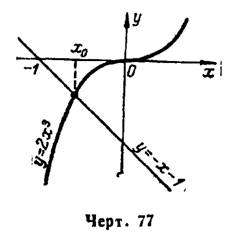
2) Преобразуя уравнение  к виду
к виду  и построив кривые
и построив кривые  и
и  в одних координатных осях (рис. 77), заключаем: данное алгебраическое уравнение имеет только один действительный корень, содержащийся на отрезке [- 0,6; -0,5].
в одних координатных осях (рис. 77), заключаем: данное алгебраическое уравнение имеет только один действительный корень, содержащийся на отрезке [- 0,6; -0,5].
3) Приводим уравнение  к виду
к виду  и построим кривые
и построим кривые  и
и  (рис. 78).
(рис. 78).
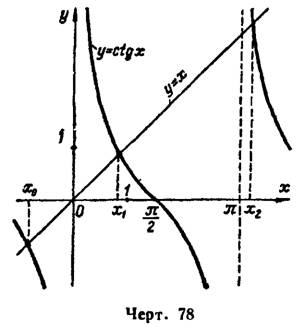
Котангенсоида имеет бесчисленное множество бесконечных ветвей, каждая из которых пересекает прямую  . Поэтому данное уравнение имеет бесчисленное множество действительных корней. Наименьший положительный корень
. Поэтому данное уравнение имеет бесчисленное множество действительных корней. Наименьший положительный корень  этого уравнения содержится на отрезке [0,8; 0,9].
этого уравнения содержится на отрезке [0,8; 0,9].







